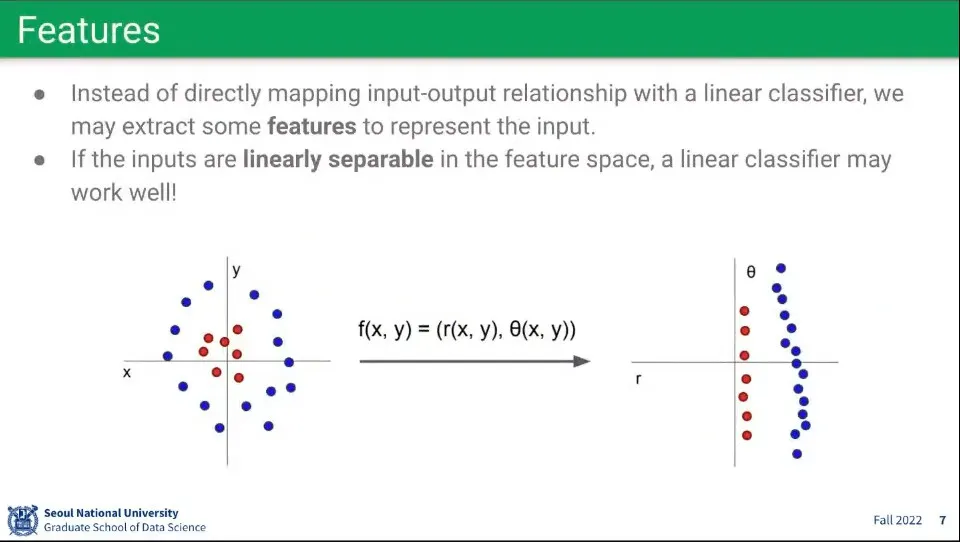
머신러닝 및 딥러닝 1/ Lecture 3. Convolutional Neural Networks

•

선형 모델로는 비선형 문제를 해결하기 어려움

◦

비선형인 데이터는 선형으로 구분할 수 없고, WWW도 1개 밖에 사용할 수 없음

•

비선형 문제를 해결하기 위해 위와 같은 방법이 사용될 수 있음. feature를 뽑은 후에 선형 모델로 처리하는 방법

◦

하지만 대부분의 문제는 그렇게 해결되지 않음

•

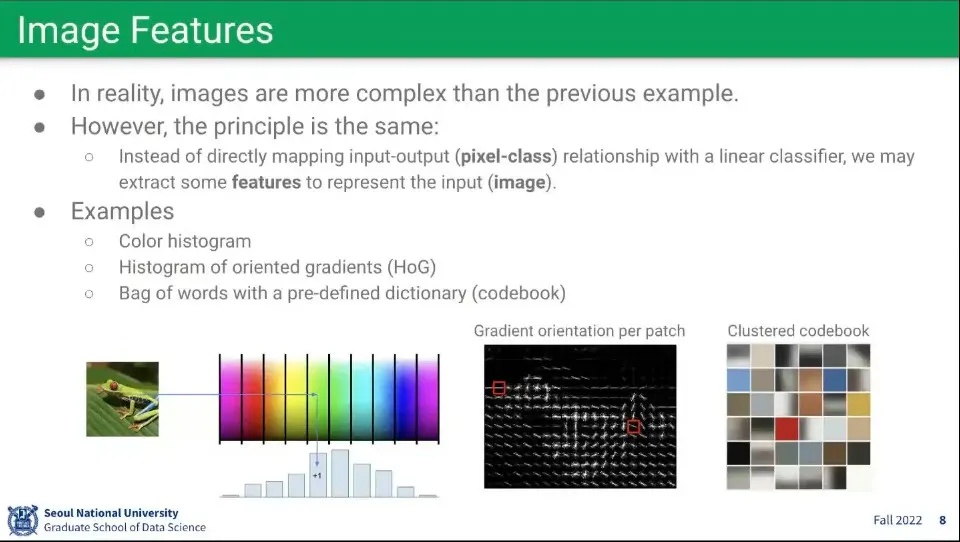
이미지에 대해 feature를 뽑는 방법. 히스토그램을 뽑는다거나 등

•

머신러닝에서 예전에는 우선 이미지에서 feature를 뽑고 그걸 학습 시켰는데, 시간이 지나고 나서 아예 feature를 뽑는 것 자체를 머신러닝에 맡기게 됨. 이게 바로 end-to-end 학습

•

그러나 이것은 별로 효율적인 방법은 아니다.

◦

데이터가 엄청 많아야 하고 그만큼 컴퓨팅 파워도 필요함. 비용이 많이 듬.

◦

사람은 이런 식으로 학습하지 않는다.

•

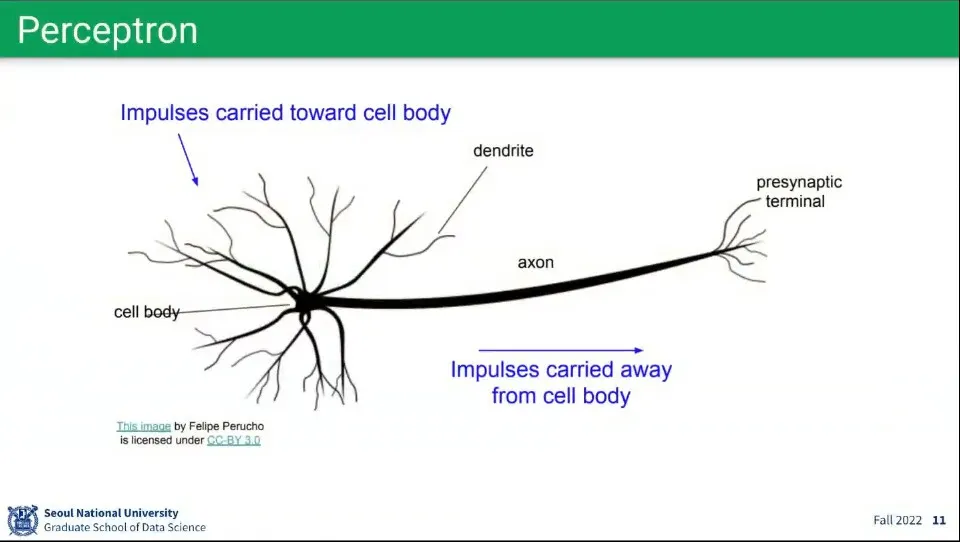
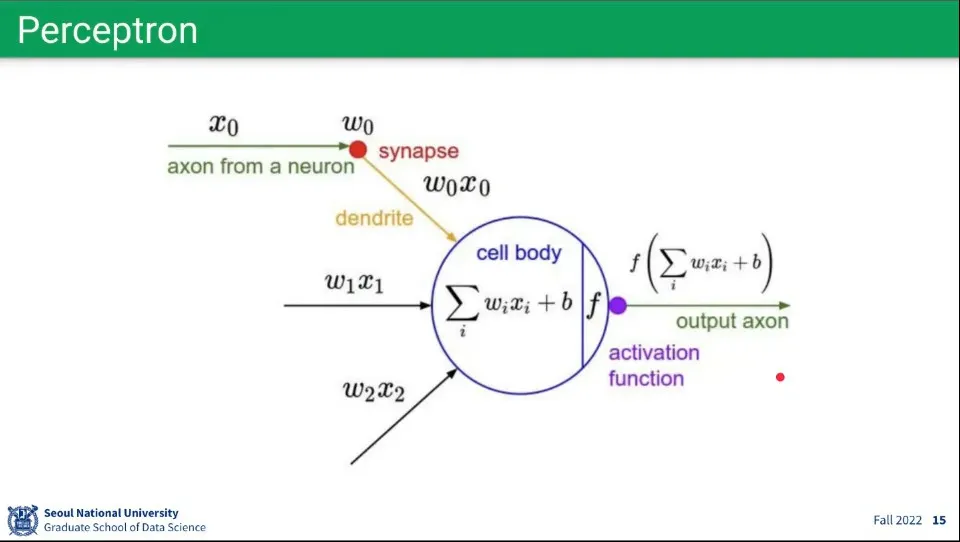
퍼셉트론은 뉴런의 모습에서 착안 함. 

◦

연결된 다른 뉴런들에 신호를 받고(input), 그게 일정 조건(activation function)을 만족하면(threshold) 다른 뉴런들에 신호를 보냄(output)

•

위 개념을 퍼셉트론을 표현한 것

◦

이전 노드 xxx들에 각각 가중치 WWW를 곱한 것을 합하고 —선형 결합

◦

그 값을 어떤 활성화 함수 fff에 통과 시켜서 결과를 얻고, 

◦

그 결과를 다음 노드들에 전달 함.

•

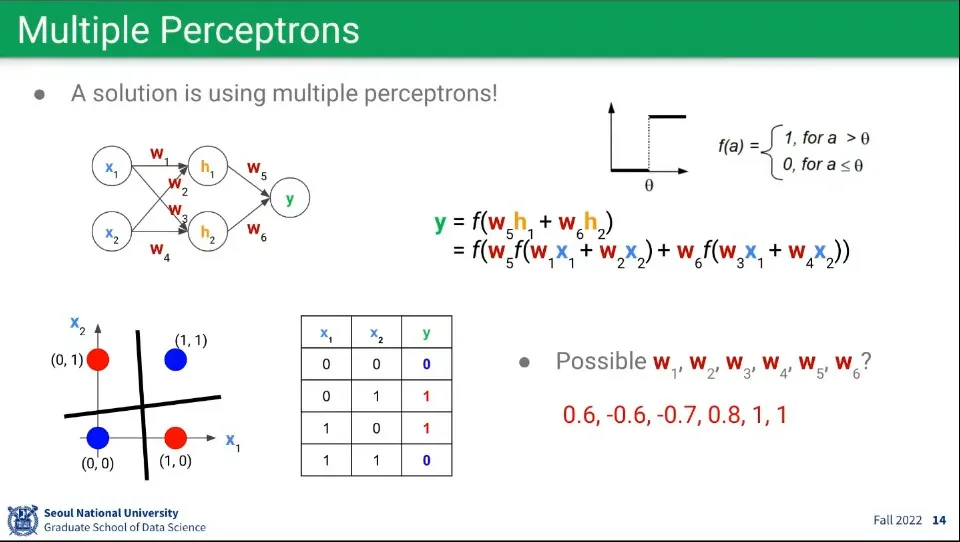
이 퍼셉트론 구조를 이용하면 논리 연산이 가능함. —예시는 AND 연산

•

그런데 이 퍼셉트론 구조만으로는 XOR 문제를 해결할 수가 없음

•

이 문제는 퍼셉트론을 여러 층으로 쌓아서 해결할 수 있음

•

수학적으로 3층의 레이어만 있으면 모든 연산이 가능하다고 한다.

•

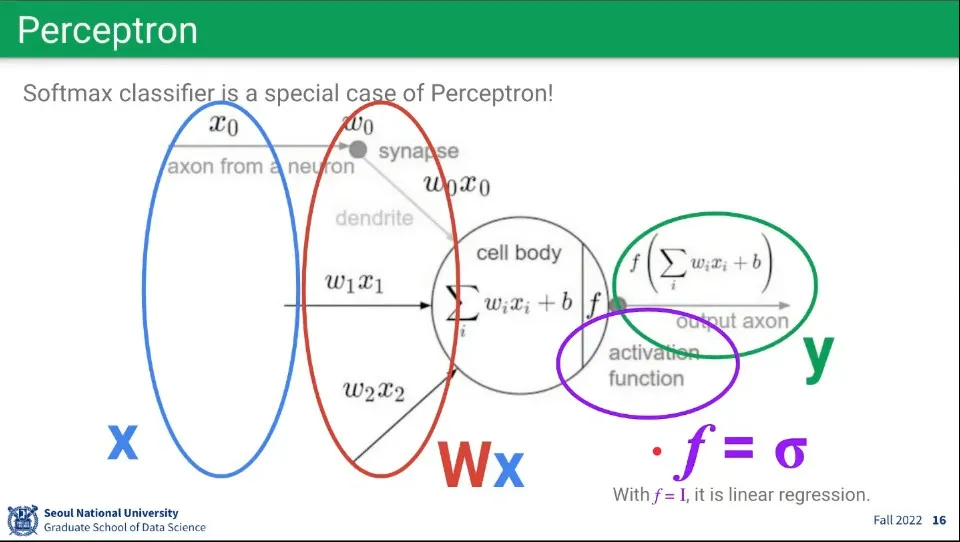
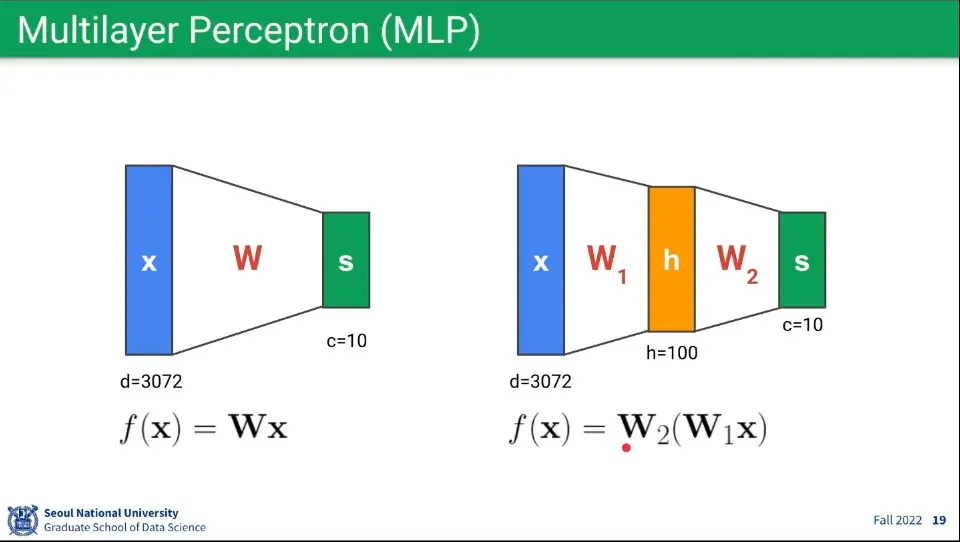
퍼셉트론은 수식으로 표현하면 위와 같다.

•

그런데 이 모습은 선형 함수와 동일하다. 퍼셉트론이 내부적으로 선형 함수를 계산하고 있는 것.

•

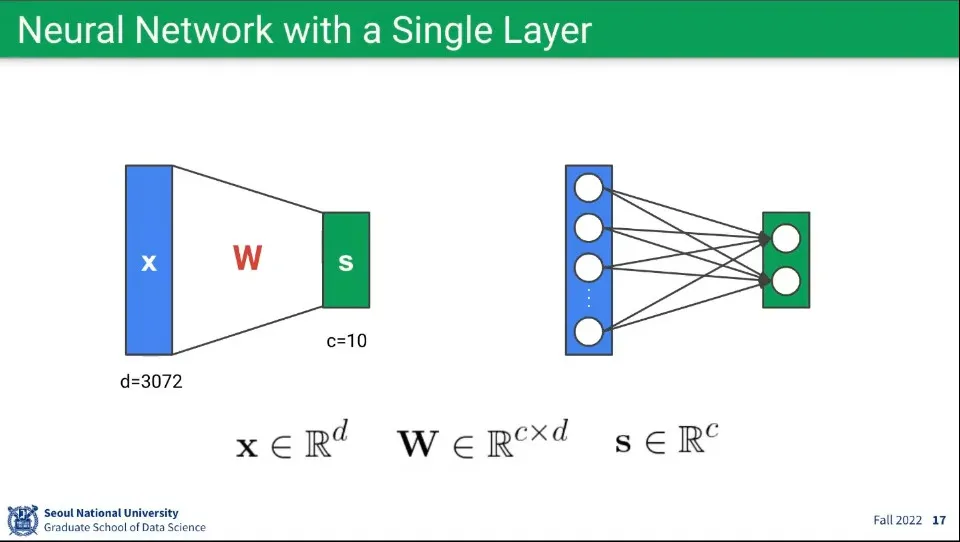
뉴럴 네트워크란 여러 개의 퍼셉트론를 연결한 것

•

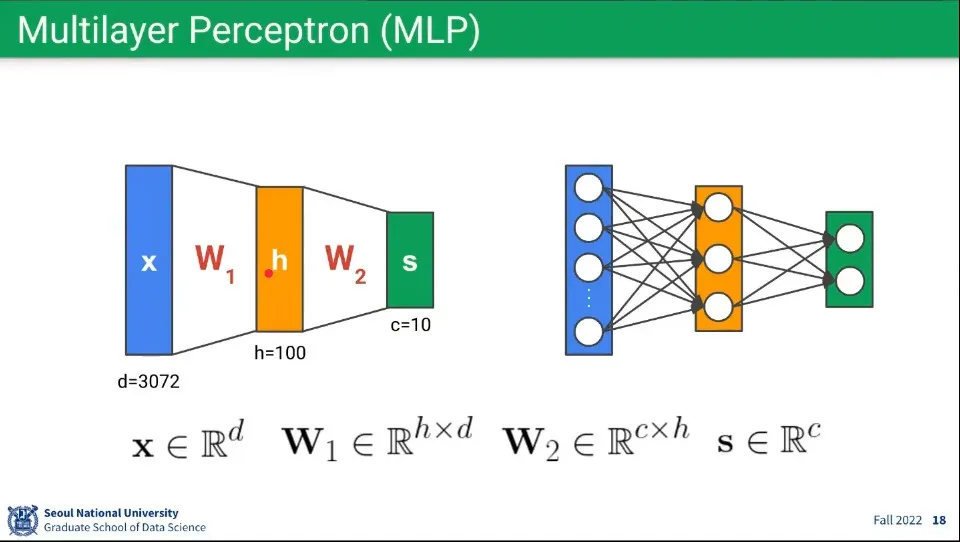
그런 퍼셉트론 레이러를 여러층으로 쌓으면 Multilayer Perceptron이 된다. 

◦

이 레이어를 여러 층으로 깊게 연결한게 딥 러닝 네트워크가 된다.

•

수학적으로 single layer나 multi layer는 행렬 계산이라는 점에서 수학적 동일하다. 

◦

위의 예시에서 W2,W1W_{2}, W_{1}W2​,W1​의 곱을 또 다른 행렬로 나타내면 결국 single layer와 동일해지기 때문.

•

그런데 어떻게 1개의 레이어에서는 안 풀리던 xor 문제가 2개 층으로 쌓으면 풀릴 수 있었을까?

•

single layer와 multi layer의 가장 큰 차이는 activation function에 있다. 이 활성화 함수 덕분에 single layer에서는 해결이 안 되는 문제가 multi layer에서는 해결이 된다.

◦

바로 이 활성화 함수가 딥러닝에서 진짜 핵심이다.

◦

활성화 함수가 없다면 single layer와 multi layer는 수학적으로 동일하다. 

•

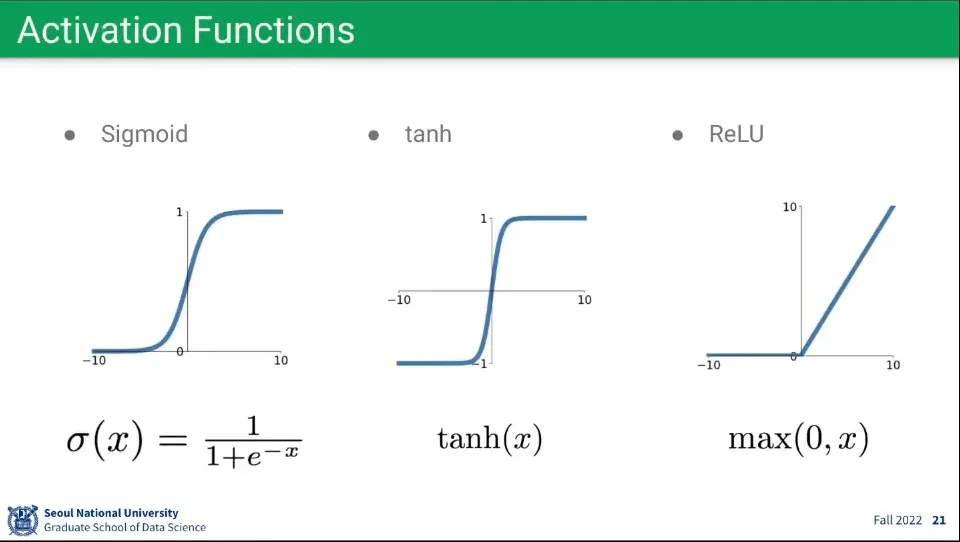
활성화 함수로는 시그모이드, 탄젠트 하이퍼볼릭, 렐루 함수를 많이 사용한다. 

•

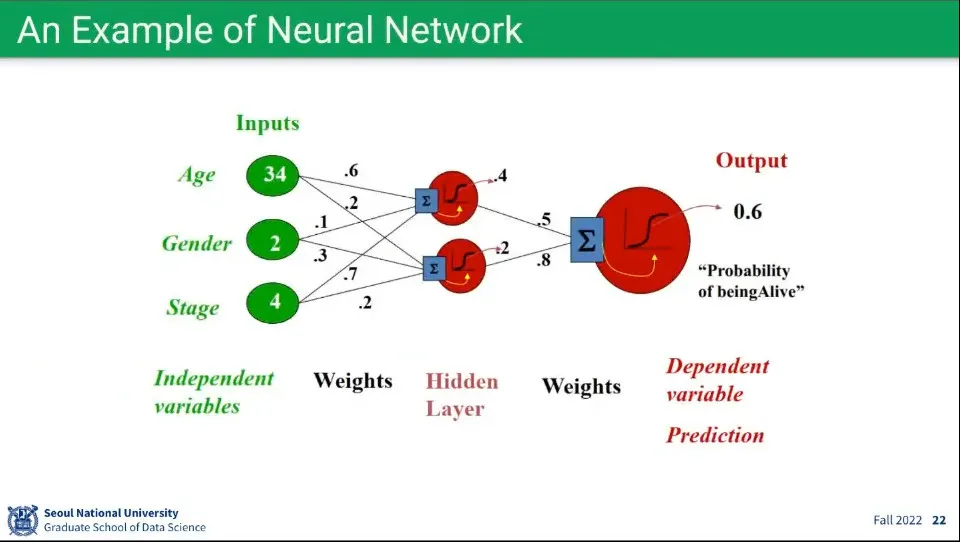
뉴럴 네트워크의 예시

•

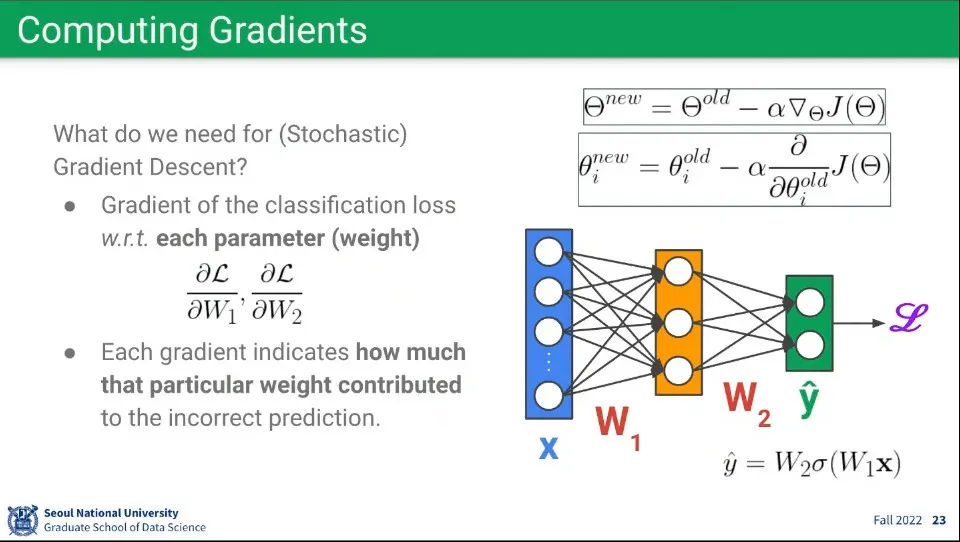
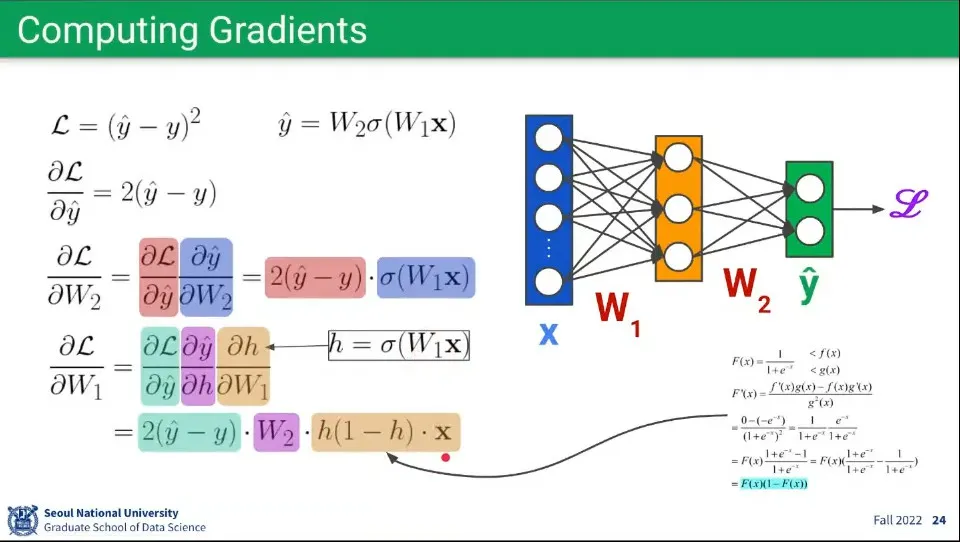
뉴럴 네트워크에 Gradient 적용하는 예시. 

◦

각 노드들이 선형 함수를 계산하고 있기 때문에 비슷하게 적용할 수 있다.

◦

다만 Loss 함수를 계산하기 위해 노드에 연결된 파라미터들에 대해 각각 편미분을 해줘야 하는 부분에 차이가 있음

•

Gradient를 구하기 위해 편미분을 구해줘야 하는데, 위와 같이 구할 수 있다. layer가 여러개 이므로 각 layer 별로 편미분을 하는데, 이때 chain rule이 적용되어서 앞 단계의 미분 결과를 이용해서 할 수 있다.

가장 오른쪽 레이어가 Loss 함수((y^−y)2(\hat{y} - y)^{2}(y^​−y)2)에 대해 y^\hat{y}y^​으로 편미분 한다. 

{\partial \mathcal{L} \over \partial \hat{y}} = 2(\hat{y} - y)

그 다음 레이어가 Loss 함수에 대해 가중치 W2W_{2}W2​로 편미분한다. 

•

이것은 Chain Rule이 적용되어서 Loss 함수를 y^\hat{y}y^​으로 편미분한 것과 y^\hat{y}y^​을 W2W_{2}W2​로 편미분한 것의 곱으로 표현할 수 있다.

{\partial \mathcal{L} \over \partial W_{2}} = {\partial \mathcal{L} \over \partial \hat{y}} {\partial \hat{y} \over \partial W_{2}} = 2(\hat{y} - y) \cdot \sigma(W_{1}x)

그 다음 레이어가 Loss 함수에 대해 가중치 W1W_{1}W1​로 편미분한다.

•

마찬가지로 Chain Rule이 적용되어서 Loss 함수를 y^\hat{y}y^​으로 편미분한 것과 y^\hat{y}y^​를 hhh —σ(W1x)\sigma(W_{1}x)σ(W1​x)— 로 편미분한 것과 hhh를 W1W_{1}W1​으로 편미분한 것을 곱하여 표현한다.

•

hhh를 W1W_{1}W1​로 편미분한 것은 eee를 미분하는 것에서 나온다.

{\partial \mathcal{L} \over \partial W_{1}} = {\partial \mathcal{L} \over \partial \hat{y}} {\partial \hat{y} \over \partial h} {\partial h \over \partial W_{1}} = 2(\hat{y} - y) \cdot W_{2} \cdot h(1-h) \cdot x

•

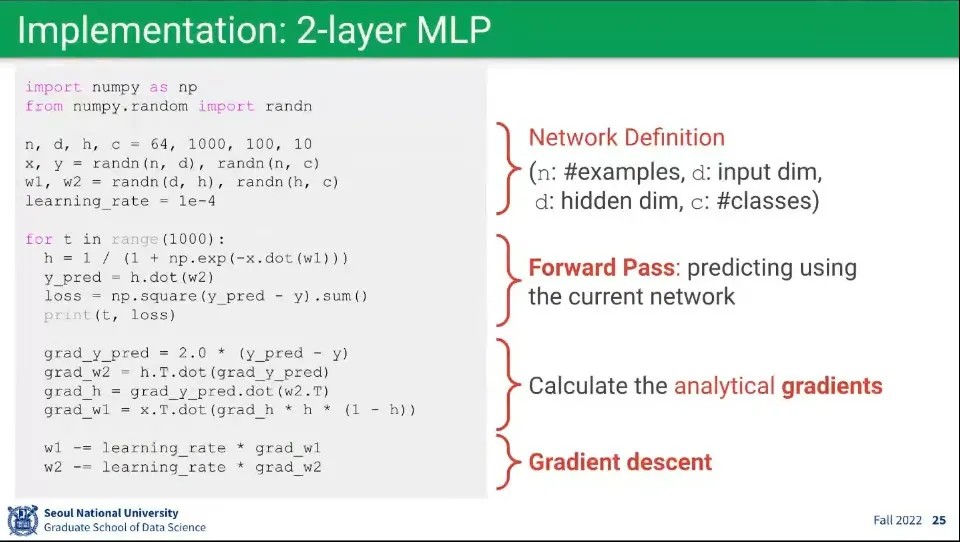
위 수식에 대한 예시 코드

Foward 계산

Loss 계산

미분값 계산

미분값에 Learning Rate를 곱해서 가중치 업데이트

•

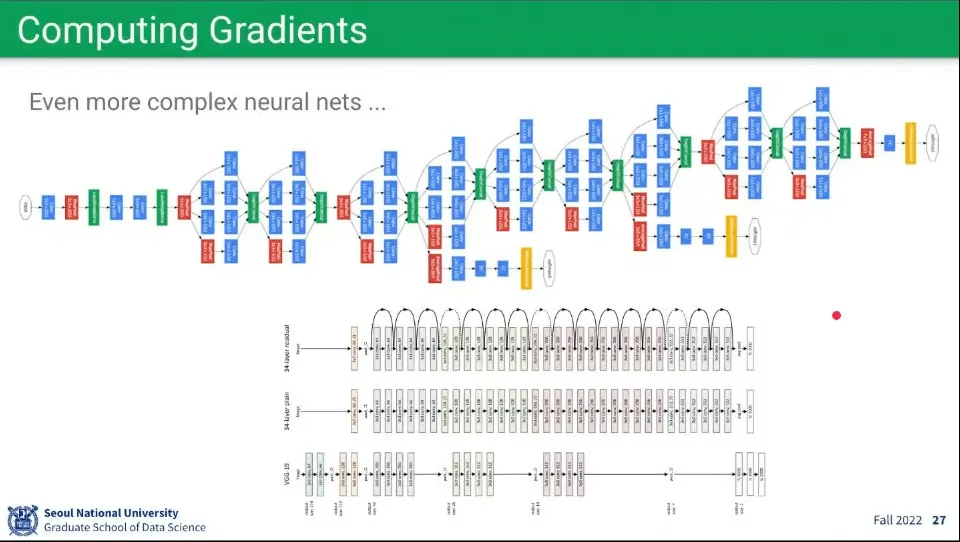
최근의 딥러닝 네트워크는 매우 깊고 복잡하기 때문에, 위 수식을 직접 계산하지는 않고, PyTorch 등에서 제공하는 라이브러리를 사용 함

•

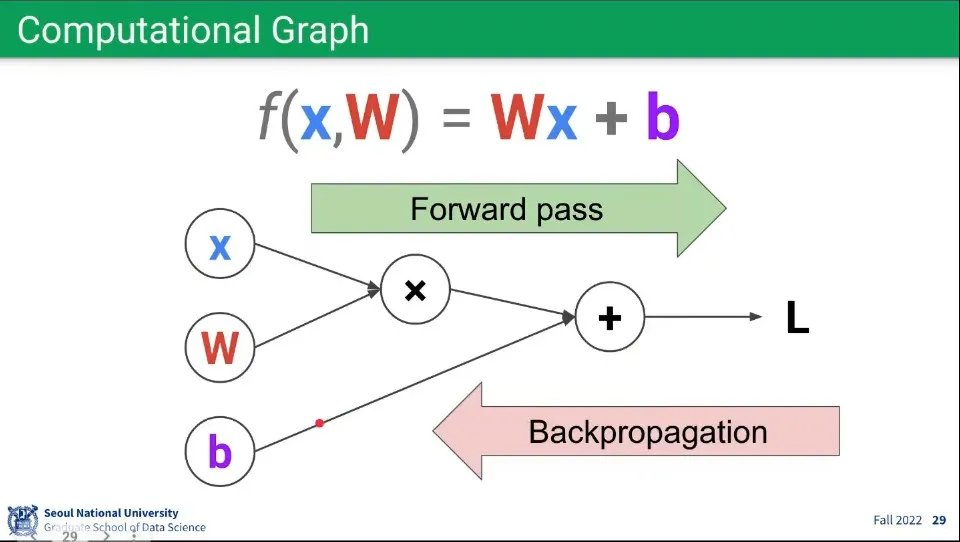
네트워크 학습의 계산은 Forward pass와 Backpropagation을 계산해 준다.

•

Backpropagation 계산 예제

◦

가장 뒤에서부터 편미분해서 그 앞의 결과를 그 뒤의 레이어가 받아서 연속적으로 계산한다.

•

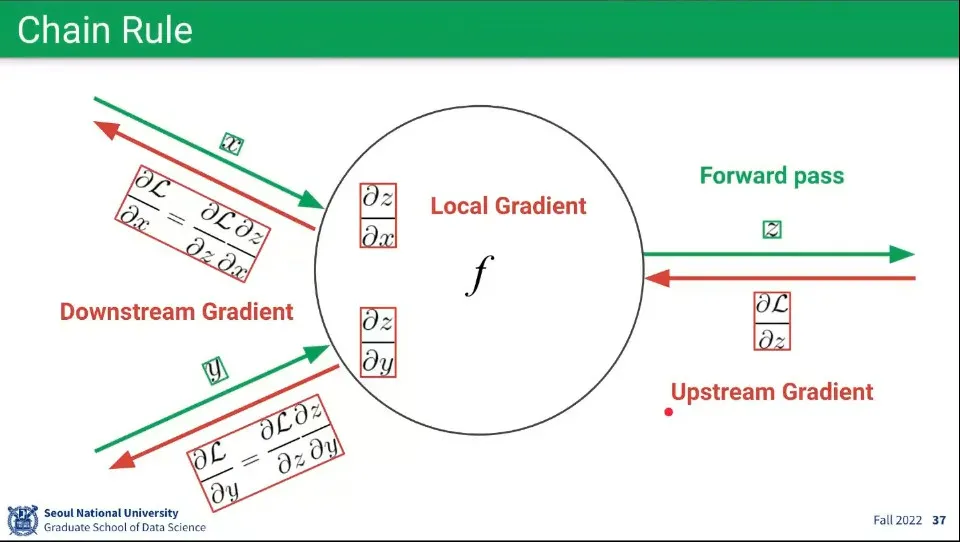
Chain Rule 예제

◦

Loss를 가중치로 편미분한 것이 Gradient인데, 다음 노드로 가는 가중치로 Loss를 편미분 한 것이 Upstream Gradient가 되고, 이전 노드에서 자기 자신에게 오는 가중치로 Loss를 편미분 한 것이 Downstream Gradient가 된다. 

◦

이전 노드의 가중치로 현재 노드의 함수를 편미분한 것을 Local Gradient라고 한다. Chain Rule에 의해 Downstream Gradient는 Upstream Gradient와 Local Gradient를 곱한 것으로 계산할 수 있다.

•

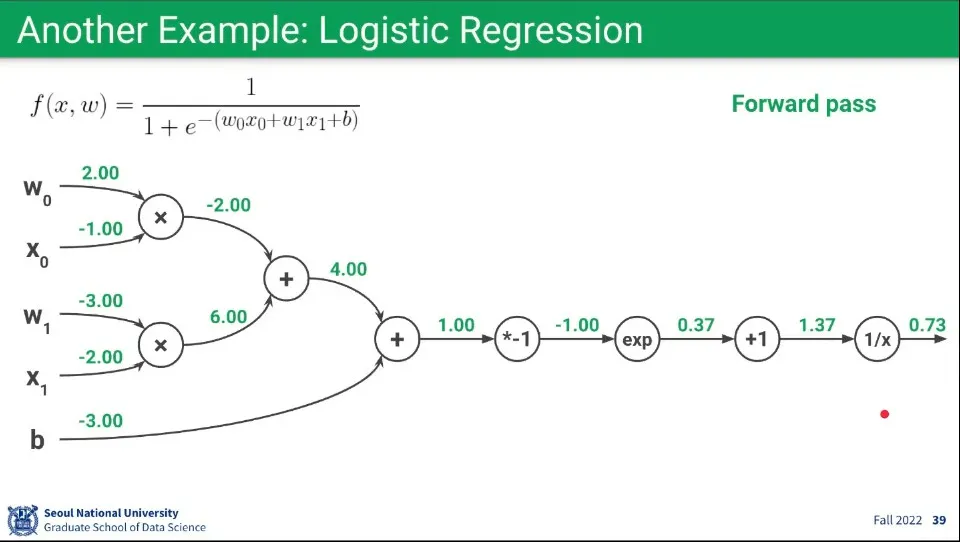
Foward 계산 예제. 

◦

예측 함수가 위와 같고, 각 파라미터의 초기값이 파라미터 왼쪽에 쓰여진 값이라고 할 때, Forward 가중치 계산 결과는 위와 같다.

•

이걸 보면 퍼셉트론이 어떻게 함수를 분해할 수 있는지를 이해할 수 있음

◦

초기값을 제외한 각 노드는 어떤 함수에 대응된다. 그 함수는 덧셈이나 곱셈, 역수, exponential 등의 연산이 가능함. —당연히 논리 연산이나 Sigmoid 등도 가능

◦

엣지는 실제 값을 가지며 이어지는 함수(노드)에 input이 된다. 이것은 Backpropagation으로 업데이트가 된다.

◦

위 식은 이항 혹은 단항 연산으로 분해 했지만, 만일 함수가 3개 이상의 파라미터를 받는 함수라면 노드가 받는 엣지는 3개 이상일 수 있다.

•

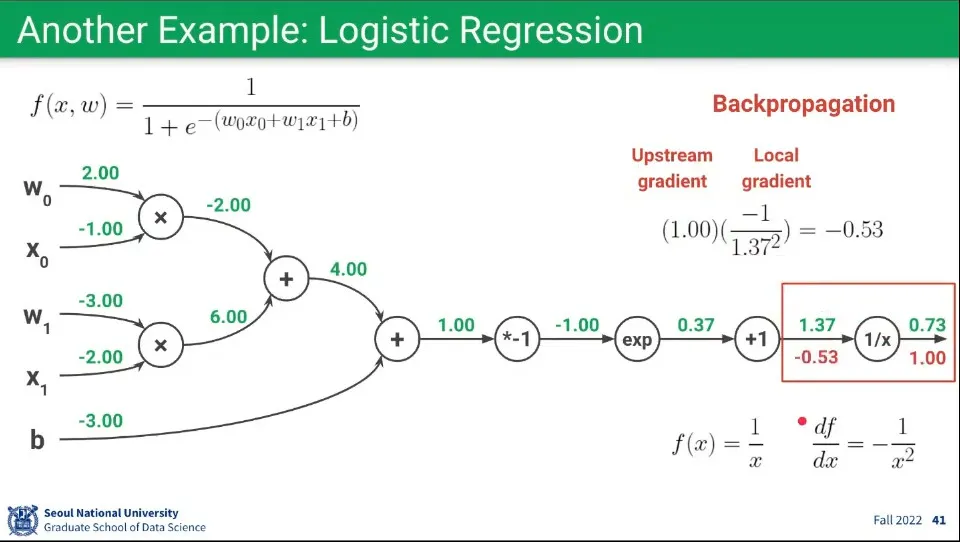
Backpropagation 예제 1

◦

일단 가장 마지막 Upstream Gradient는 1로 계산한다. 이것은 기본 사항이다.

◦

가장 마지막 바로 앞의 노드의 함수는 f(x)=1xf(x) = {1 \over x}f(x)=x1​이고, 이를 xxx로 편미분하면 dfdx=−1x2{df \over dx} = - {1 \over x^{2}}dxdf​=−x21​이 된다. 

◦

이렇게 구해진 함수에 Forward 때 구한 1.371.371.37을 대입해서 최종적으로 Local Gradient −11.372- {1 \over 1.37^{2}}−1.3721​를 구한다.

◦

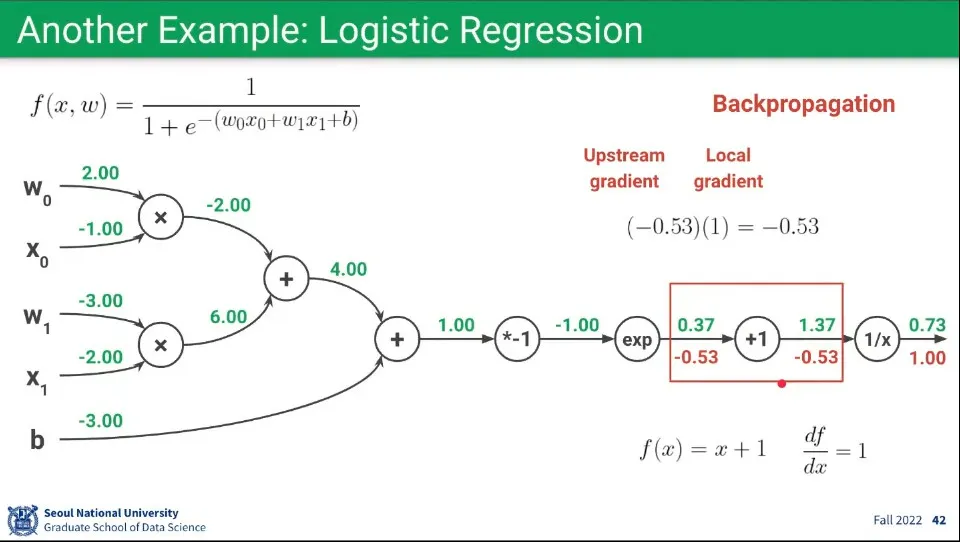
Downstream Gradient는 Upstream Gradient와 Local Gradient의 곱이기 때문에 앞서 구한 두 값을 곱해 최종적으로 1×−11.372=−0.531 \times {-1 \over 1.37^{2}} = -0.531×1.372−1​=−0.53의 값을 구한다.

•

Backpropagation 예제 2

◦

앞의 과정을 반복하여 현재 노드의 함수 f(x)=x+1f(x) = x + 1f(x)=x+1를, xxx로 편미분 하면 dfdx=1{df \over dx} = 1dxdf​=1을 구할 수 있다.

◦

상수가 나왔으므로 대입 없이 Local Gradient는 111로 계산한다.

◦

Upstream Gradient는 앞서 −0.53-0.53−0.53으로 구했으므로 이 둘을 곱해 −0.53×1=−0.53-0.53 \times 1 = -0.53−0.53×1=−0.53을 구한다.

•

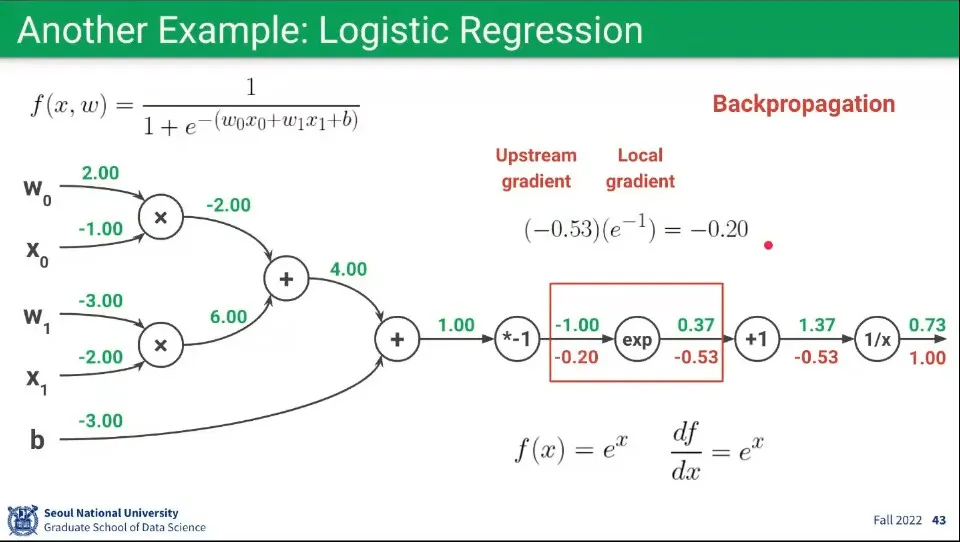
Backpropagation 예제 3

◦

앞의 과정을 반복하여 현재 노드의 함수 f(x)=exf(x) = e^{x}f(x)=ex을 xxx로 편미분하면 dfdx=ex{df \over dx} = e^{x}dxdf​=ex을 구할 수 있다.

◦

이렇게 구해진 함수에 Forward에서 구한 −1-1−1를 대입해서 최종적으로 e−1e^{-1}e−1를 구한다. 

◦

Upstream Gradient는 앞서 −0.53-0.53−0.53으로 구했으므로 이 둘을 곱해 −0.53×e−1=−0.2-0.53 \times e^{-1} = -0.2−0.53×e−1=−0.2을 구한다.

•

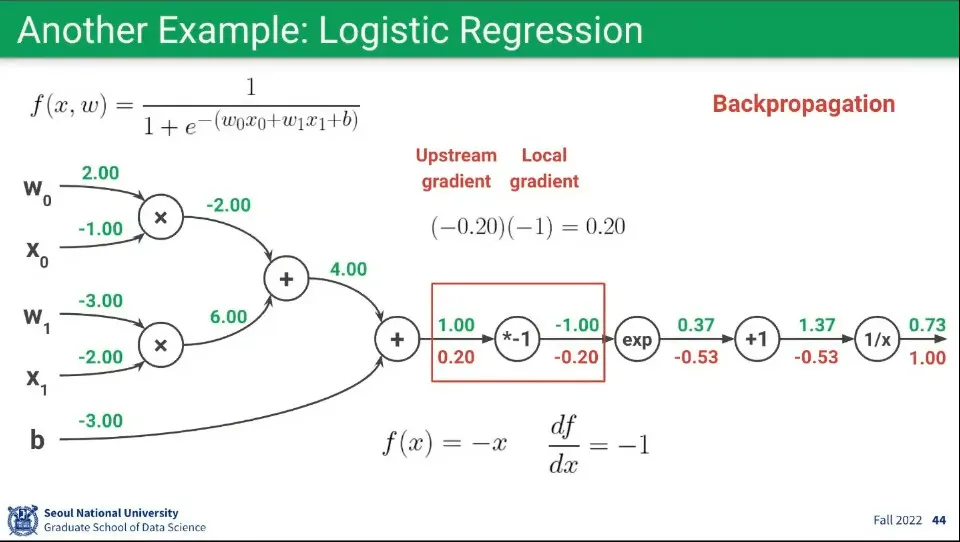
Backpropagation 예제 4

◦

앞의 과정을 반복하여 현재 노드의 함수 f(x)=−xf(x) = -xf(x)=−x를 xxx로 편미분하면 dfdx=−1{df \over dx} = -1dxdf​=−1을 구할 수 있다.

◦

상수가 나왔으므로 대입 없이 Local Gradient는 −1-1−1로 계산한다.

◦

Upstream Gradient는 앞서 −0.2-0.2−0.2으로 구했으므로 이 둘을 곱해 −0.2×−1=0.2-0.2 \times -1 = 0.2−0.2×−1=0.2을 구한다.

•

Backpropagation 예제 5

◦

앞의 과정을 반복하여 현재 노드의 함수 f(x,y)=x+yf(x, y) = x + yf(x,y)=x+y를 xxx로 편미분하면 dfdx=1{df \over dx} = 1dxdf​=1이 되고, yyy로 편미분 하면 dfdy=1{df \over dy} = 1dydf​=1이 된다. 

◦

두 편미분 모두 상수가 나왔으므로 대입 없이 Local Gradient는 111로 계산한다.

◦

Upstream Gradient는 앞서 0.20.20.2으로 구했으므로 이 둘을 곱해 0.2×1=0.20.2 \times 1 = 0.20.2×1=0.2을 구한다.

◦

두 Downstream의 편미분 값이 동일하므로 두 경로 모두 0.20.20.2를 받는다.

•

Backpropagation 예제 6

◦

이것은 L5번과 완전히 동일하며 두 경로 모두 0.20.20.2를 받는다.

•

Backpropagation 예제 7

◦

앞의 과정을 반복하여 현재 노드의 함수 f(w,x)=wxf(w, x) = wxf(w,x)=wx를 xxx로 편미분하면 dfdx=w{df \over dx} = wdxdf​=w가 되고, www로 편미분 하면 dfdw=x{df \over dw} = xdwdf​=x가 된다. 

◦

www에 대해 xxx의 Forward값 −1-1−1을 대입하여 Local Gradient −1-1−1을 구하고, 이를 Upstream Gradient 0.20.20.2에 곱해 최종적으로 −1×0.2=−0.2-1 \times 0.2 = -0.2−1×0.2=−0.2를 받는다.

◦

xxx에 대해 www의 Forward값 222을 대입하여 Local Gradient 222을 구하고, 이를 Upstream Gradient 0.20.20.2에 곱해 최종적으로 2×0.2=0.42 \times 0.2 = 0.42×0.2=0.4를 받는다.

•

Backpropagation 예제 8

◦

7번 과정과 동일하지만, x,wx, wx,w의 Forward 값이 다르므로 그것만 다르게 적용한다.

◦

www에 대해 xxx의 Forward값 −2-2−2을 대입하여 Local Gradient −2-2−2을 구하고, 이를 Upstream Gradient 0.20.20.2에 곱해 최종적으로 −2×0.2=−0.4-2 \times 0.2 = -0.4−2×0.2=−0.4를 받는다.

◦

xxx에 대해 www의 Forward값 −3-3−3을 대입하여 Local Gradient −3-3−3을 구하고, 이를 Upstream Gradient 0.20.20.2에 곱해 최종적으로 −3×0.2=−0.6-3 \times 0.2 = -0.6−3×0.2=−0.6를 받는다.

•

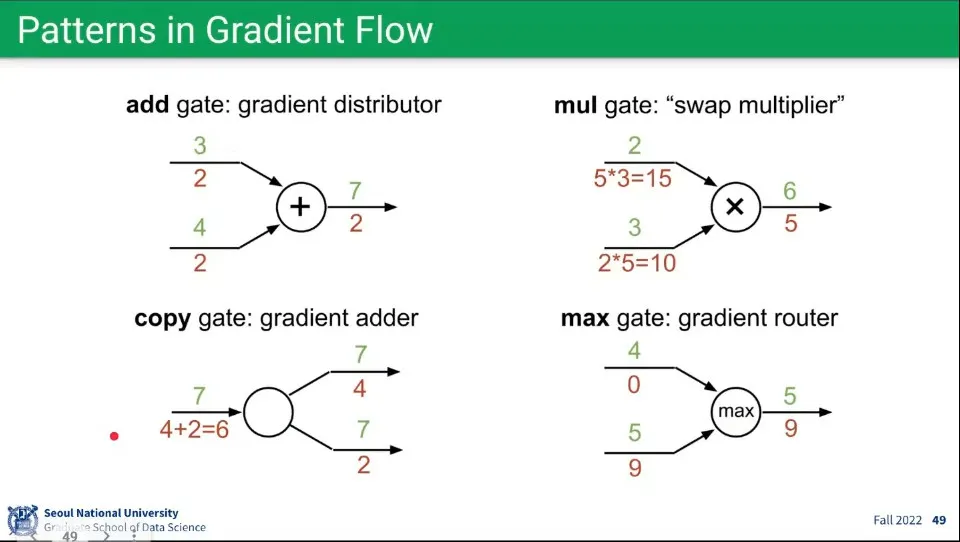
위와 같은 과정을 따라가면 각 연산에 다음과 같은 패턴이 발견된다.

◦

더하기 연산 

▪

Backward에서 Upstream의 값을 같이 받음

◦

곱하기 연산 

▪

Backward에서 반대편의 값을 Upstream에 곱해서 받음

◦

복사 연산

▪

Backward에서 Upstream들의 값을 더해서 받음

◦

Max 연산

▪

Foward일 때 Max였던 것만 Backward에서 값을 받고, 그렇지 않은 것은 0을 받음

•

앞선 예에 대한 코드 구현

•

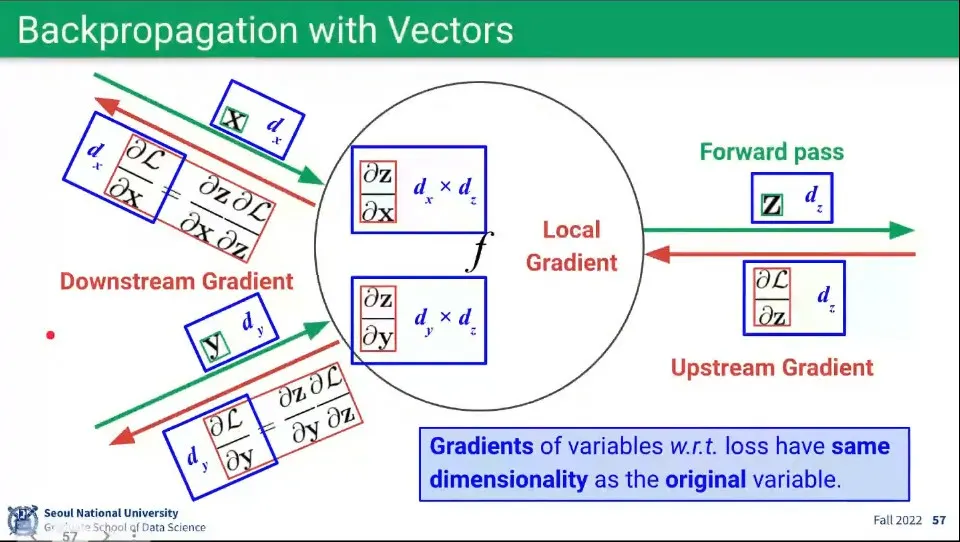
앞서와 같은 연산을 Vector에 대해서도 동일하게 할 수 있다. 

◦

다만 Vector이므로 그만큼 연산량이 많아짐.

•

연산의 과정은 앞선 것과 동일하다. 

◦

다만 Vector 연산이기 때문에 Local Gradient의 경우 행렬이 만들어진다.

▪

들어오는 벡터 dxd_{x}dx​와 나가는 벡터 dzd_{z}dz​의 곱이 되므로 dx×dzd_{x} \times d_{z}dx​×dz​ 행렬이 만들어짐

◦

Local Gradient는 행렬이 되지만, Downstream Gradient를 구할 때 Upstream Gradient를 곱하면서 차원이 상쇄되므로 Downstream Gradient는 다시 벡터가 된다.

▪

Local Gradient dx×dzd_{x} \times d_{z}dx​×dz​와 Upstream Gradient dz×1d_{z} \times 1dz​×1이 곱해져서 Downstream Gradient는 최종적으로 dx×1d_{x} \times 1dx​×1이 된다. 

•

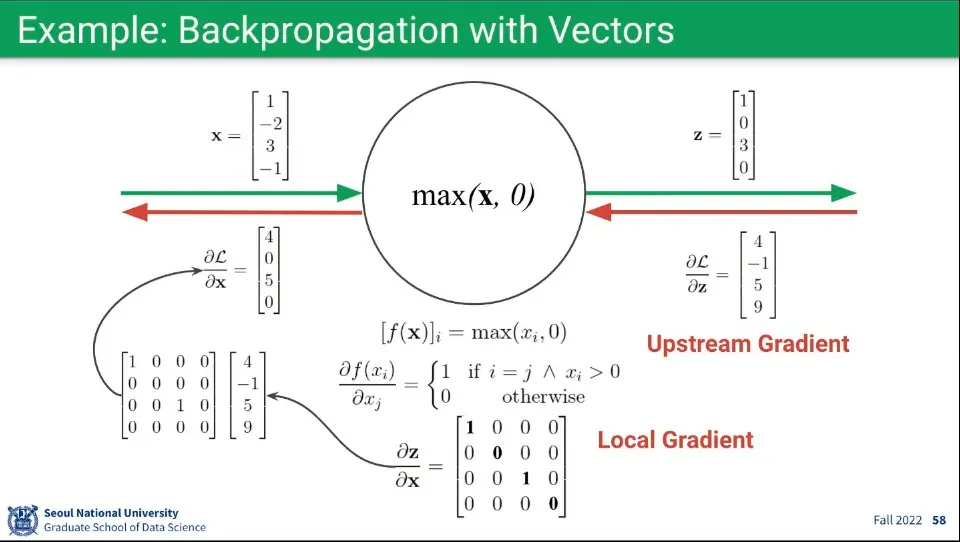
Vector로 된 연산의 예

◦

Foward와 Backward 모두 차원의 크기는 동일하다.

◦

위의 예시는 max⁡(x,0)\max(x, 0)max(x,0)의 함수가 편미분되는 부분이 좀 복잡함.

•

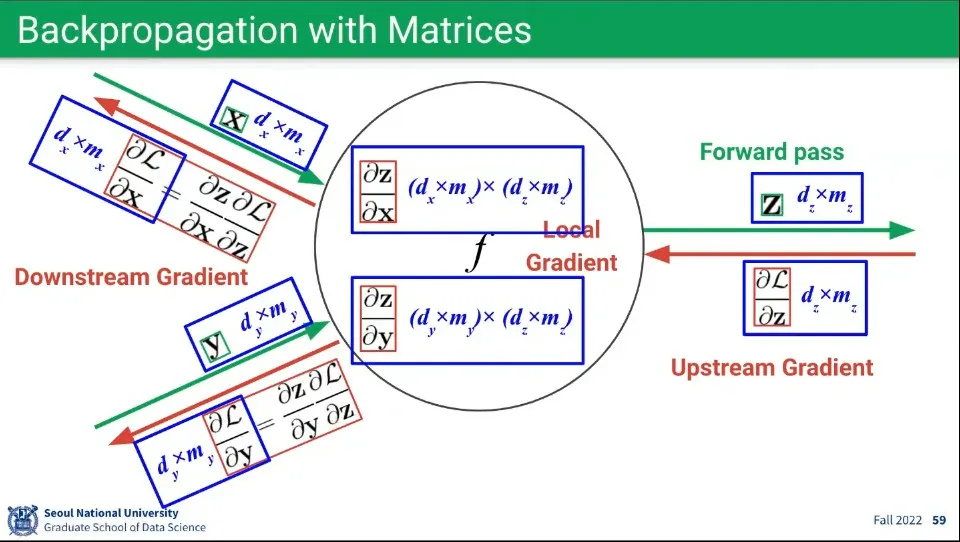
행렬에 대해서도 내용은 동일하다.

◦

다만 행렬 연산이기 때문에 Local Gradient의 경우 행렬 x 행렬이 만들어진다.

▪

들어오는 행렬 dx×mxd_{x} \times m_{x}dx​×mx​와 나가는 행렬 dz×mzd_{z} \times m_{z}dz​×mz​의 곱이 되므로 (dx×mx)×(dz×mz)(d_{x} \times m_{x}) \times (d_{z} \times m_{z})(dx​×mx​)×(dz​×mz​) 행렬이 만들어짐

◦

Local Gradient는 행렬 x 행렬이 되지만, Downstream Gradient를 구할 때 Upstream Gradient를 곱하면서 차원이 상쇄되므로 Downstream Gradient는 다시 행렬이 된다.

▪

Local Gradient (dx×mx)×(dz×mz)(d_{x} \times m_{x}) \times (d_{z} \times m_{z})(dx​×mx​)×(dz​×mz​)와 Upstream Gradient dz×mzd_{z} \times m_{z}dz​×mz​이 곱해져서 Downstream Gradient는 최종적으로 dx×mxd_{x} \times m_{x}dx​×mx​이 된다. 