Missing Data
•
데이터 벡터 의 일부에 알 수 없는 누락된 데이터가 있을 수 있다. (supervised 문제라면 feature 벡터에 라벨을 추가한다) 를 누락된 부분이라고 하고 를 관찰된 부분이라고 하자.
◦
데이터가 누락된 이유가 유익할 수 있으므로(예컨대 ‘질병 X를 갖고 계십니까?’와 같은 질문에 대답을 거부하는 것은 피험자가 실제로 질병을 앓고 있다는 표시일 수 있음) 누락된 데이터를 모델링해야 한다.
◦
이를 위해 의 어느 부분이 ‘공개(관찰)’ 되는지 여부를 나타내는 무작위 변수 을 도입한다. 구체적으로 이 관찰되는 인덱스(구성 요소)에 대해서는 을 설정하고 다른 인덱스에 대해서는 을 설정한다.
•
누락된 데이터 메커니즘에 대해 다양한 종류의 가정을 할 수 있다.
◦
가장 강력한 가정은 데이터가 missing completely at random(MCAR)이다. 이것은 을 뜻한다. 따라서 누락은 은닉이나 관찰된 feature에 의존하지 않는다.
◦
더 현실적인 가정은 missing at random(MAR)이다. 이것은 를 뜻한다. 따라서 누락은 은닉 feature에 의존하지 않지만 visible feature에 의존할 수 있다.
◦
이 두 가지 가정이 모두 성립하지 않으면 missing not at random(MNAR)이라 한다.
•
이제 형식의 모델을 사용하여 관찰된 입력 이 주어지면 결과 를 모델링하는 조건부 또는 판별 모델의 경우를 고려하자.
◦
에 조건부이기 때문에 항상 관찰된다고 가정한다. 그러나 출력 라벨은 의 값에 의존하여 관찰되지 않을 수도 있다.
◦
예컨대 semi-supervised learning에서 라벨링 데이터 와 라벨링되지 않은 데이터 의 조합을 갖는다.
•
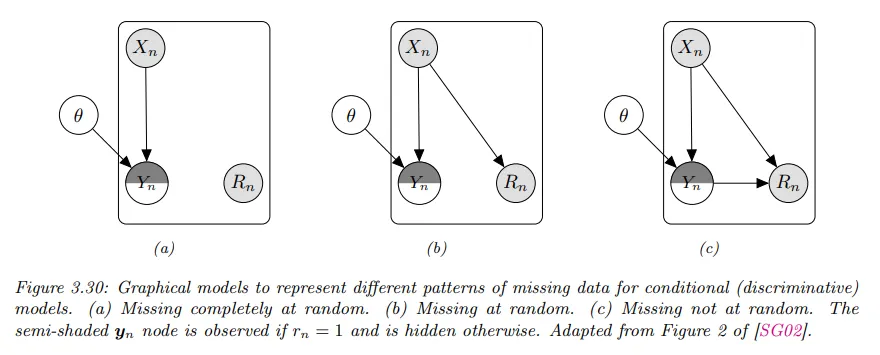
아래 그림 graphical 모델 표기를 사용하여 판별 설정에 대해 3개 누락 데이터 시나리오를 보여준다.
◦
MCAR와 MCAR 경우에 알려지지 않은 모델 파라미터 가 은닉 leaf node인 경우가 에 의해 영향을 받지 않기 때문에 출력값이 누락된 라벨이 없는 데이터는 무시할 수 있음을 볼 수 있다.
◦
그러나 MNAR 경우에 가 항상 관찰되는 의 확률에 영향을 받는다고 가정했기 때문에 숨겨진 경우에도 에 의존하는 것을 볼 수 있다. 이런 경우에 모델을 맞추기 위해 EM 같은 방법을 사용하여 누락 값을 추정해야 한다.
•
이제 형식의 판별 모델 대신 형식의 결합 또는 생성 모델을 사용하는 경우를 고려하자.
◦
이 경우에 라벨링되지 않은 데이터는 가 와 에 모두 의존하기 때문에 MCAR와 MAR 시나리오에서도 학습에 유용할 수 있다. 특히 에 관한 정보는 에 관해 유용할 수 있다.