Search
Duplicate

수학/ Integral Pobability Metrics(IPM), Maximum mean discrepancy (MMD)

Integral probability metrics

•
integral probability metric(IPM)은 P−QP-Q의 측면에서 두 분포 사이의 다이버전스를 계산한다. 다음과 같이 정의된다.
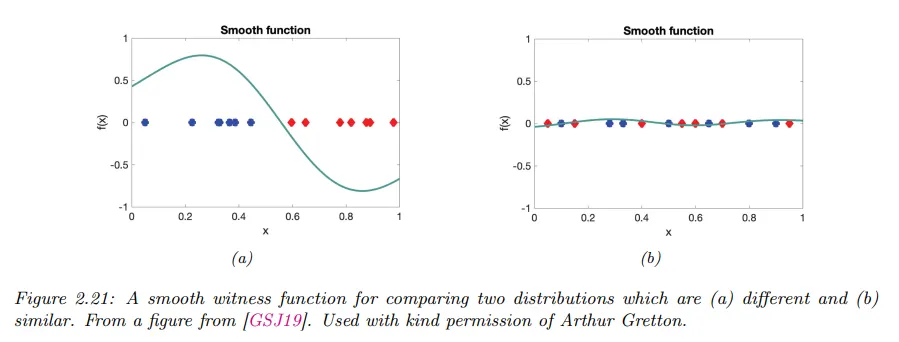
DF(P,Q)≜sup⁡f∈F∣Ep(x)[f(x)]−Eq(x′)[f(x′)]∣D_\mathcal{F}(P,Q) \triangleq \sup_{f \in \mathcal{F}}|\mathbb{E}_{p(\bold{x})}[f(\bold{x})] - \mathbb{E}_{q(\bold{x}')}[f(\bold{x}')]|
•
여기서 F\mathcal{F}는 smooth 함수의 클래스이다. 두 기대값 사이의 차이를 최대화하는 함수 ff를 witness function이라 부른다. 아래 그림 참조.
•
함수 클래스 F\mathcal{F}를 정의하는 몇 가지 방법이 있다.
◦
한 가지 접근은 양의 정부호 커널 함수로 정의된 RKHS를 사용하는 것이다. 이것은 maximum mean discrepancy(MMD, 최대 평균 불일치)로 알려진 방법을 발생시킨다.
•
또 다른 방법은 bounded Lipschitz 상수를 갖는 함수들의 집합으로 F\mathcal{F}를 정의하는 것이다. 즉 F={∥f∥L≤1}\mathcal{F} = \{\|f\|_L \le 1\}. 여기서
∥f∥L=sup⁡x≠x′∣f(x)−f(x′)∣∥x−x′∥\|f\|_L = \sup_{\bold{x} \ne \bold{x}'}{|f(\bold{x}) - f(\bold{x}')| \over \|\bold{x} - \bold{x}'\|}
•
이 경우에 IPM은 Wasserstein-1 distance와 같아진다.
W1(P,Q)≜sup⁡∥f∥L≤1∣Ep(x)[f(x)]−Eq(x′)[f(x′)]∣W_1(P,Q) \triangleq \sup_{\|f\|_L \le1}|\mathbb{E}_{p(\bold{x})}[f(\bold{x})]-\mathbb{E}_{q(\bold{x}')}[f(\bold{x}')]|

Maximum mean discrepancy (MMD)

•
maximum mean discrepancy(MMD)는 두 분포의 샘플을 사용하여 불일치 측정값 D(P,Q)D(P,Q)를 정의하는 방법이다.
◦
샘플은 고차원 입력을 다룰 수 있는 양의 정부호 커널을 사용하여 비교된다.
◦
이 접근은 2-샘플 테스트를 정의하고 암시적 생성 모델을 훈련하는데 사용될 수 있다.

MMD as an IPM

•
MMD는 다음 형식의 적분 확률 메트릭(integral probability metric, IPM)이다.
◦
(여기서 sup⁡\sup은 supremum의 약자로 집합의 상한(upper bound)의 최소값을 나타낸다. 이것의 반대는 infimum의 약자인 inf⁡\inf가 있다. 이것은 집합의 하한(lower bound)의 최대값을 나타낸다.)
MMD(P,Q;F)=sup⁡f∈F:∥f∥≤1[Ep(x)[f(x)]−Eq(x′)[f(x′)]]\text{MMD}(P,Q;\mathcal{F}) = \sup_{f \in \mathcal{F}:\|f\|\le1}\left[\mathbb{E}_{p(\bold{x})}[f(\bold{x})]- \mathbb{E}_{q(\bold{x}')}[f(\bold{x}')]\right]
•
여기서 F\mathcal{F}는 양의 정부호 커널 함수 K\mathcal{K}로 정의된 RKHS이다. 이 집합의 함수를 기저 함수의 무한 합으로 표현할 수 있다.
f(x)=⟨f,ϕ(x)⟩F=∑l=1∞flϕl(x)f(\bold{x}) = \langle f, \phi(\bold{x})\rangle_\mathcal{F} = \sum_{l=1}^\infty f_l\phi_l(\bold{x})
•
witness 함수 ff의 집합을 이 RKHS의 단위 공 안에 있도록 제한한다. 따라서 ∥f∥F2=∑l=1∞fl2≤1\|f\|_\mathcal{F}^2 = \sum_{l=1}^\infty f_l^2 \le 1.
•
기대의 선형성으로 다음을 갖는다.
Ep(x)[f(x)]=⟨f,Ep(x)[ϕ(x)]⟩F=⟨f,μP⟩F\mathbb{E}_{p(\bold{x})}[f(\bold{x})] = \langle f, \mathbb{E}_{p(\bold{x})}[\phi(\bold{x})]\rangle_\mathcal{F} = \langle f, \boldsymbol{\mu}_P\rangle_\mathcal{F}
•
여기서 μP\boldsymbol{\mu}_P는 분포 PP의 kernel mean embedding이라고 한다. 따라서
MMD(P,Q;F)=sup⁡∥f∥≤1⟨f,μP−μQ⟩F=μP−μQ∥μP−μQ∥\text{MMD}(P,Q;\mathcal{F}) = \sup_{\|f\|\le 1}\langle f, \boldsymbol{\mu}_P- \boldsymbol{\mu}_Q\rangle_\mathcal{F} = {\boldsymbol{\mu}_P - \boldsymbol{\mu}_Q \over \|\boldsymbol{\mu}_P - \boldsymbol{\mu}_Q\|}
•
내적을 최대화하는 단위 벡터 f\bold{f}는 feature 평균의 차이와 평행하기 때문이다.
•
직관을 얻기 위해 ϕ(x)=[x,x2]\boldsymbol{\phi}(x) = [x,x^2]을 가정하자.
◦
이 경우에 MMD는 두 분포의 첫 두 모멘트의 차이를 계산한다. 이것은 모든 가능한 분포를 구별하는데 충분하지 않다. 그러나 가우시안 커널을 사용하는 것은 두 개의 무한하게 큰 feature 벡터를 비교하는 것과 동등하므로 두 분포의 모든 모멘트를 효과적으로 비교할 수 있다.
◦
사실 non-degenerate 커널을 사용하면 P=QP=Q이면 MMD=0\text{MMD} = 0임을 보일 수 있고 그 역도 성립한다.

Computing the MMD using the kernel trick

•
이 섹션에서 두 개의 샘플 집합 X={xn}n=1N,X′={xm′}m=1M\mathcal{X} = \{\bold{x}_n\}_{n=1}^N, \mathcal{X}'= \{\bold{x}'_m\}_{m=1}^M (여기서 xn∼P\bold{x}_n \sim P이고 xm′∼Q\bold{x}'_m \sim Q이다)이 주어졌을 때 방정식 MMD(P,Q;F)\text{MMD}(P,Q;\mathcal{F})을 실제로 어떻게 계산하는지 설명한다.
◦
μP=1N∑n=1Nϕ(xn)\boldsymbol{\mu}_P = {1\over N} \sum_{n=1}^N \boldsymbol{\phi}(\bold{x}_n)와 μQ=1M∑m=1Mϕ(xm′)\boldsymbol{\mu}_Q = {1\over M} \sum_{m=1}^M \boldsymbol{\phi}(\bold{x}'_m)를 두 분포의 커널 평균 임베딩의 경험적 추정치라고 하자. 그러면 제곱 MMD는 다음과 같이 주어진다.
MMD2(X,X′)≜∥1N∑n=1Nϕ(xn)−1M∑m=1Mϕ(xm′)∥2=1N2∑n=1N∑n′=1Nϕ(xn)⊤ϕ(xn′)−2NM∑n=1N∑m=1Mϕ(xn)⊤ϕ(xm′)+1M2∑m=1M∑m′=1Mϕ(xm′′)⊤ϕ(xm′)\begin{aligned} \text{MMD}^2(\mathcal{X},\mathcal{X}') &\triangleq \|{1\over N} \sum_{n=1}^N \boldsymbol{\phi}(\bold{x}_n) - {1\over M} \sum_{m=1}^M \boldsymbol{\phi}(\bold{x}'_m)\|^2 \\ &= {1\over N^2} \sum_{n=1}^N \sum_{n'=1}^N\boldsymbol{\phi}(\bold{x}_n)^\top\boldsymbol{\phi}(\bold{x}_{n'}) - {2 \over NM} \sum_{n=1}^N \sum_{m=1}^M \boldsymbol{\phi}(\bold{x}_n)^\top \boldsymbol{\phi}(\bold{x}'_m) \\ &+ {1\over M^2}\sum_{m=1}^M \sum_{m'=1}^M \boldsymbol{\phi}(\bold{x}'_{m'})^\top\boldsymbol{\phi}(\bold{x}'_m) \end{aligned}
•
위 방정식이 feature 벡터의 내적만 포함하기 때문에 커널 트릭을 사용하여 다음처럼 재작성할 수 있다.
MMD2(X,X2)=1N2∑n=1N∑n′=1NK(xn,xn′)−2NM∑n=1N∑m=1MK(xn,xm′)+1M2∑m=1M∑m′=1MK(xm′,xm′′)\text{MMD}^2(\mathcal{X},\mathcal{X}^2) = {1\over N^2}\sum_{n=1}^N \sum_{n'=1}^N \mathcal{K}(\bold{x}_n,\bold{x}_{n'}) - {2 \over NM} \sum_{n=1}^N \sum_{m=1}^M \mathcal{K}(\bold{x}_n,\bold{x}'_m) \\+ {1\over M^2}\sum_{m=1}^M \sum_{m'=1}^M \mathcal{K}(\bold{x}'_m,\bold{x}'_{m'})

Linear time computation

•
MMD는 계산에 O(N2)O(N^2)시간이 걸린다. 여기서 NN은 각 분포의 샘플들의 수이다.
◦
O(N)O(N)시간이 걸리는 unnormalized mean embedding(UME)라고 부르는 다른 테스트 통계가 제시되었다. 핵심 아이디어는 다음을 평가하는 것이다.
witness2(v)=(μQ(v)−μP(v))2\text{witness}^2(\bold{v}) = (\boldsymbol{\mu}_Q(\bold{v})-\boldsymbol{\mu}_P(\bold{v}))^2
•
테스트 위치 집합 v1,...,vj\bold{v}_1,...,\bold{v}_j은 PP와 QQ 사이의 차이를 감지하는데 충분하다. 따라서 (제곱) UME를 다음처럼 정의한다.
UME2(P,Q)=1J∑j=1J[μP(vj)−μQ(vj)]2\text{UME}^2(P,Q) = {1\over J}\sum_{j=1}^J [\boldsymbol{\mu}_P(\bold{v}_j) - \boldsymbol{\mu}_Q(\bold{v}_j)]^2
•
여기서 μP(v)=Ep(x)[K(x,v)]\boldsymbol{\mu}_P(\bold{v}) = \mathbb{E}_{p(\bold{x})}[\mathcal{K}(\bold{x},\bold{v})]는 경험적으로 O(N)O(N) 시간에 추정될 수 있다. 그리고 μQ(v)\boldsymbol{\mu}_Q(\bold{v})도 유사하다.
•
UME의 normalized 버전은 NME라고 한다.
◦
NME를 위치 vj\bold{v}_j에 관해 최대화하면 테스트의 통계적 검정력을 최대화하고 PP와 QQ가 가장 차이나는 위치를 찾을 수 있다.
◦
이것은 고차원 데이터에 대해 해석 가능한 2-샘플 테스트를 제공한다.

Choosing the right kernel

•
MMD(와 UME)의 효율성은 커널의 올바른 선택에 전적으로 의존한다. 1차원 샘플을 구별하는 것에서도 커널의 선택은 매우 중요하다.
◦
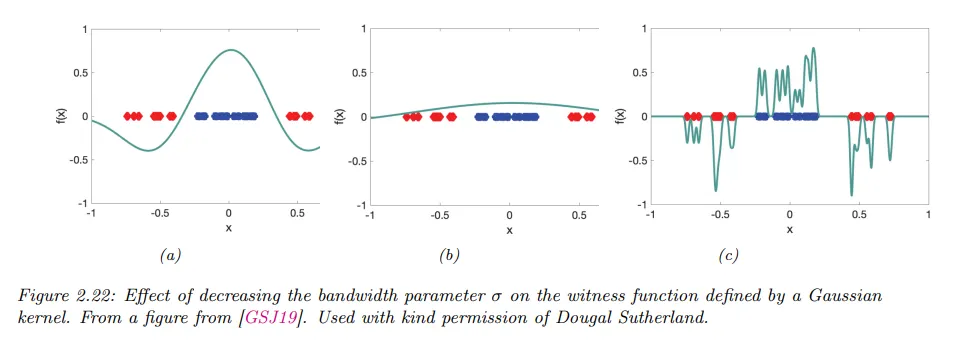
예컨대 가우시안 커널 Kσ(x,x′)=exp⁡(−12σ2∥x−x′∥2)\mathcal{K}_\sigma(\bold{x},\bold{x}') = \exp(-{1\over 2\sigma^2}\|\bold{x}-\bold{x}'\|^2)를 고려하자. σ\sigma를 변화시키는 것의 효과는 1차원 샘플의 서로 다른 2개의 다른 집합을 구별하는 능력의 측면에서 아래 그림에 나타난다.
◦
다행히 MMD는 커널 파라미터에 관해 미분 가능하다. 따라서 테스트의 검정력을 최대화하기 위해 최적의 σ2\sigma^2를 선택할 수 있다.
•
이미지와 같은 고차원 데이터에 대해 pre-trained CNN 모델을 저차원 feature를 계산하는 방법으로 사용하는 것은 유용할 수 있다.
◦
예컨대 K(x,x′)=Kσ(h(x),h(x′))\mathcal{K}(\bold{x},\bold{x}') = \mathcal{K}_\sigma(\bold{h}(\bold{x}), \bold{h}(\bold{x}'))를 정의할 수 이다. 여기서 h\bold{h}는 ‘inception’ 모델과 같은 CNN의 어떤 은닉 레이어이다.
◦
결과 MMD 메트릭은 kernel inception distance라고 한다. 이것은 Frechet inception instance와 유사한데, 통계적 속성이 더 우수하고 인간의 인지 판단과 더 나은 상관관계를 보인다.

참고

Made with