Search
Duplicate

수학/ Exponential, Inverse Gamma, Pareto 분포

Exponential distribution

•
exponential distribution은 감마 분포의 특별한 경우로 다음과 같이 정의된다.
Expon(x∣λ)≜Ga(x∣shape=1,rate=λ)\text{Expon}(x|\lambda) \triangleq \text{Ga}(x|\text{shape} = 1, \text{rate} = \lambda)
•
이 분포는 푸아송 프로세스 즉, 사건이 상수 average rate λ\lambda로 연속적이고 독립적으로 발생하는 프로세스에서 사건 사이의 시간을 설명한다.

Chi-squared distribution

•
chi-squared 분포는 감마 분포의 특별한 경우로 다음과 같이 정의된다.
χν2(x)≜Ga(x∣shape=ν2,rate=12)\chi_\nu^2(x) \triangleq \text{Ga}(x|\text{shape}= {\nu \over 2}, \text{rate} = {1\over2})
•
여기서 ν\nu는 자유도(degrees of freedom)이다. 이 분포는 제곱 가우시안 확률 변수의 합이다.
◦
더 정확하게 Zi∼N(0,1)Z_i \sim \mathcal{N}(0,1)이고 S=∑i=1νZi2S = \sum_{i=1}^\nu Z_i^2이면 S∼χν2S \sim \chi_\nu^2이다. 따라서 X∼N(0,σ2)X \sim \mathcal{N}(0, \sigma^2)이면 X2∼σ2χ12X^2 \sim \sigma^2\chi_1^2.
◦
E[χ12]=1\mathbb{E}[\chi_1^2] = 1이고 V[χ12]=2\mathbb{V}[\chi_1^2] = 2이기 때문에 다음이 성립한다.
E[X2]=σ2,V[X2]=2σ4\mathbb{E}[X^2] = \sigma^2, \mathbb{V}[X^2] = 2\sigma^4

Inverse gamma

•
inverse gamma 분포는 X∼Ga(a,b)X \sim \text{Ga}(a,b)을 가정하여 Y=1/XY = 1/X의 분포이다. Y∼IG(a,b)Y \sim \text{IG}(a,b)로 표기한다. pdf는 다음과 같이 정의된다.
IG(x∣shape=a,scale=b)≜baΓ(a)x−(a+1)e−b/x\text{IG}(x|\text{shape} = a, \text{scale} = b) \triangleq {b^a \over \Gamma(a)}x^{-(a+1)}e^{-b/x}
•
평균은 a>1a > 1일 때만 존재하고 분산은 a>2a > 2일 때만 존재한다.
•
scaled inverse chi-squared 분포는 inverse gamma 분포의 reparametrization 한 것이다.
χ−2(x∣ν,σ2)=IG(x∣shape=ν2,scale=νσ22)=1Γ(ν/2)(νσ22)ν/2x−ν2−1exp⁡(−νσ22x)\begin{aligned} \chi^{-2}(x|\nu,\sigma^2) &= \text{IG}(x|\text{shape} = {\nu \over 2}, \text{scale} = {\nu\sigma^2 \over 2}) \\ &= {1 \over \Gamma(\nu/2)} \left({\nu\sigma^2 \over 2}\right)^{\nu/2} x^{-{\nu \over 2} -1}\exp\left(-{\nu \sigma^2 \over 2x} \right) \end{aligned}
•
χν−2(x)\chi_\nu^{-2}(x)로 작성되는 일반 inverse chi-squared 분포는 νσ2=1\nu\sigma^2 = 1인 특별한 경우이다. (즉 σ2=1/ν\sigma^2 = 1/\nu). 이것은 IG(x∣shape=ν/2,scale=12)\text{IG}(x|\text{shape} = \nu/2, \text{scale} = {1\over2})에 해당한다.

Pareto distribution

•
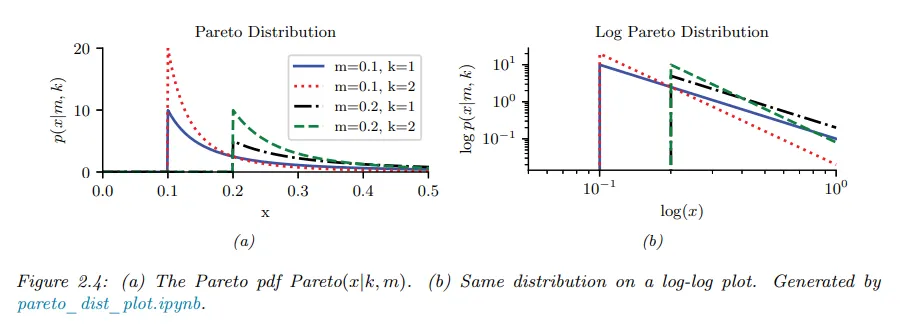
Pareto 분포는 다음의 pdf을 갖는다.
Pareto(x∣m,κ)=κmκ1x(κ+1)I(x≥m)\text{Pareto}(x|m,\kappa) = \kappa m^\kappa{1\over x^{(\kappa+1)}} \mathbb{I}(x \ge m)
•
아래 그림 (a) 참조. xx가 최소값 mm보다 크지만 그 이후에는 pdf가 급격히 감소하는 것을 볼 수 있다.
◦
log-log scale로 분포를 plot 하면 직선 log⁡p(x)=−alog⁡x+log⁡(c)\log p(x) = -a \log x + \log (c)가 된다. 여기서 a=(κ+1)a = (\kappa + 1)이고 c=κmκc = \kappa m^\kappa. 아래 그림 (b) 참조.
•
m=0m = 0에서 분포는 p(x)=κx−ap(x) = \kappa x^{-a} 형식을 갖고 이것은 멱 법칙(power law)이라고 한다.
◦
a=1a=1이면 분포는 p(x)∝1/xp(x) \propto 1/x 형식이 되는데, xx를 주파수로 해석하면 이것은 1/f1/f 함수라고 부른다.
•
파레토 분포는 대부분의 값은 작지만 작은 수의 매우 큰 값이 존재하는 heavy tails나 long tails가 나타나는 수량의 분포를 모델링하는데 유용하다. 많은 데이터의 형식이 이 속성을 나타낸다.
◦
많은 데이터셋이 다양한 latent factor에 의해 생성되며, 이러한 요인들이 함께 섞이면 자연스럽게 무거운 꼬리를 가진 분포가 만들어지기 때문이라고 주장하기도 한다.
•
파레토 분포는 이탈리아의 경제학자이자 사회학자인 Vilfredo Pareto의 이름을 따서 붙여졌다. 그는 여러 나라에 걸쳐 부의 분포를 모델링하기 위해 이것을 만들었다.
◦
사실 경제학에서 파라미터 κ\kappa는 Pareto Index라 불린다. κ=1.16\kappa = 1.16을 설정하면 80-20 rule을 커버한다. 이것은 한 사회의 부의 80%를 인구의 20%가 보유한다는 뜻이다.
•
Zipf’s 법칙에 따르면 언어에서 가장 빈번하게 사용되는 단어는 (’the’ 같은) 2번째로 빈번하게 사용되는 단어 (’of’ 같은)에 대해 약 2배가 되고, 2번째 빈번하게 사용되는 단어는 다시 4번째로 사용되는 단어의 2배가 되는 현상이 나타난다. 이것은 다음 형식의 파레토 분포에 해당한다.
p(x=r)∝κr−ap(x=r) \propto \kappa r^{-a}
•
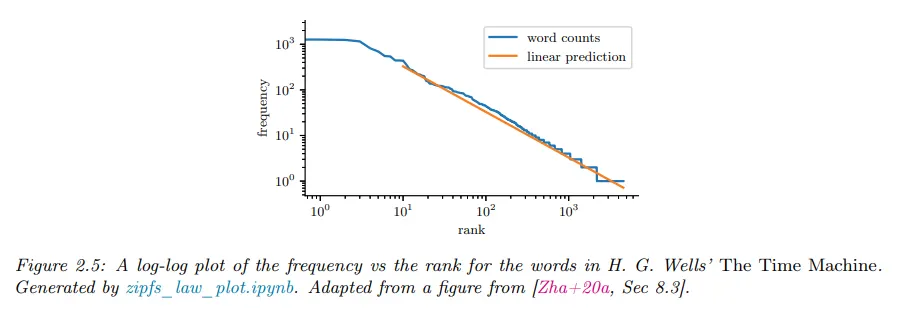
여기서 rr은 빈도수로 정렬했을 때 단어 xx의 랭크이다. κ\kappa와 aa는 상수이다. a=1a = 1을 설정하면 Zipf’s 법칙을 복구한다.
◦
따라서 Zipf’s 법칙은 ‘log 빈도수 단어 vs 그것의 log rank’를 plot 하면 기울기 −1-1의 직선이 될 것이라고 예측한다. 이것은 사실이다. 아래 그림 참조.

참조

Made with